SOLVING STATISTIC AND PROBABILITY

In solving the statistics and probability use the formula ” Z= x- μ/σ “. The ” x “ is the value , the ” μ ” is the mean, while the ” σ ” is the standard deviation.

Sample Problem:
              A survey found out that the battery life of a gadget last for 3 years and the standard deviation is 1 year. What is the probability the battery life of gadget will last between 3 and 4 years.


Step 1:  Read and understand the problem.
Step 2:  Identify the variable
               The variable presented by a capital letter ” X “ .

Example:
                      X = Battery life

Step 3: List the given information/ data from the problem.
Example:
                  μ = mean = 3 years
                  x = value  = 3 and 4 years
                 σ = standard deviation  =  1 year
(Noted):
             The mean can be a probability, percentage and chances.

Step 4: Express in symbols what is being asked in the problem.

Example:
                 P( 3 < X < 4 )
(Noted):
              Use the capital letter ” X” because it is normal distribution.

Step 5: Draw the curve
Example: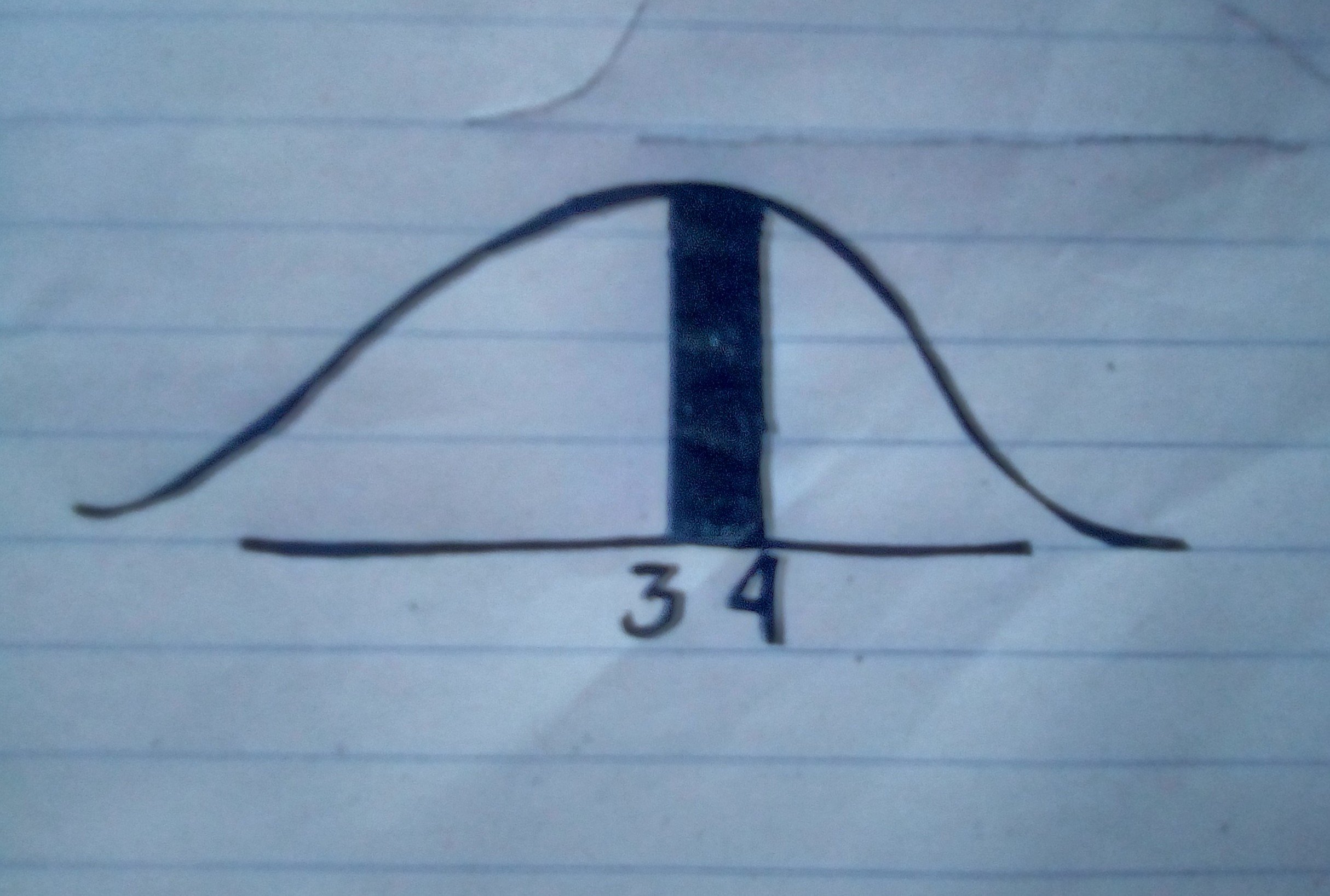(Noted) :
               In normal distribution the center of the curve is the given mean not zero ( 0 ).

Step 6: Convert the normal distribution into standard normal distribution by computing the ” Z – scores ” use the given formula.

Example:
        Z= x- μ/σ.                       Z= x- μ/σ
          = 3 – 3 ÷ 1                       = 4 – 3 ÷ 1
          = 0 ÷1                              = 1 ÷ 1
          = 0                                   = 1
(Noted) :
           Use two solutions because the problem ask for two possible probability but if not just use one solution.

Step 7: Expressed what is being asked in standard normal symbol.

Example:
            P( 0 < Z < 1 )
( Noted ):
                 Transfer ” X ” into ” Z ” and use the corresponding Z – scores.

Step 8: Draw the standardized normal curved.
Example: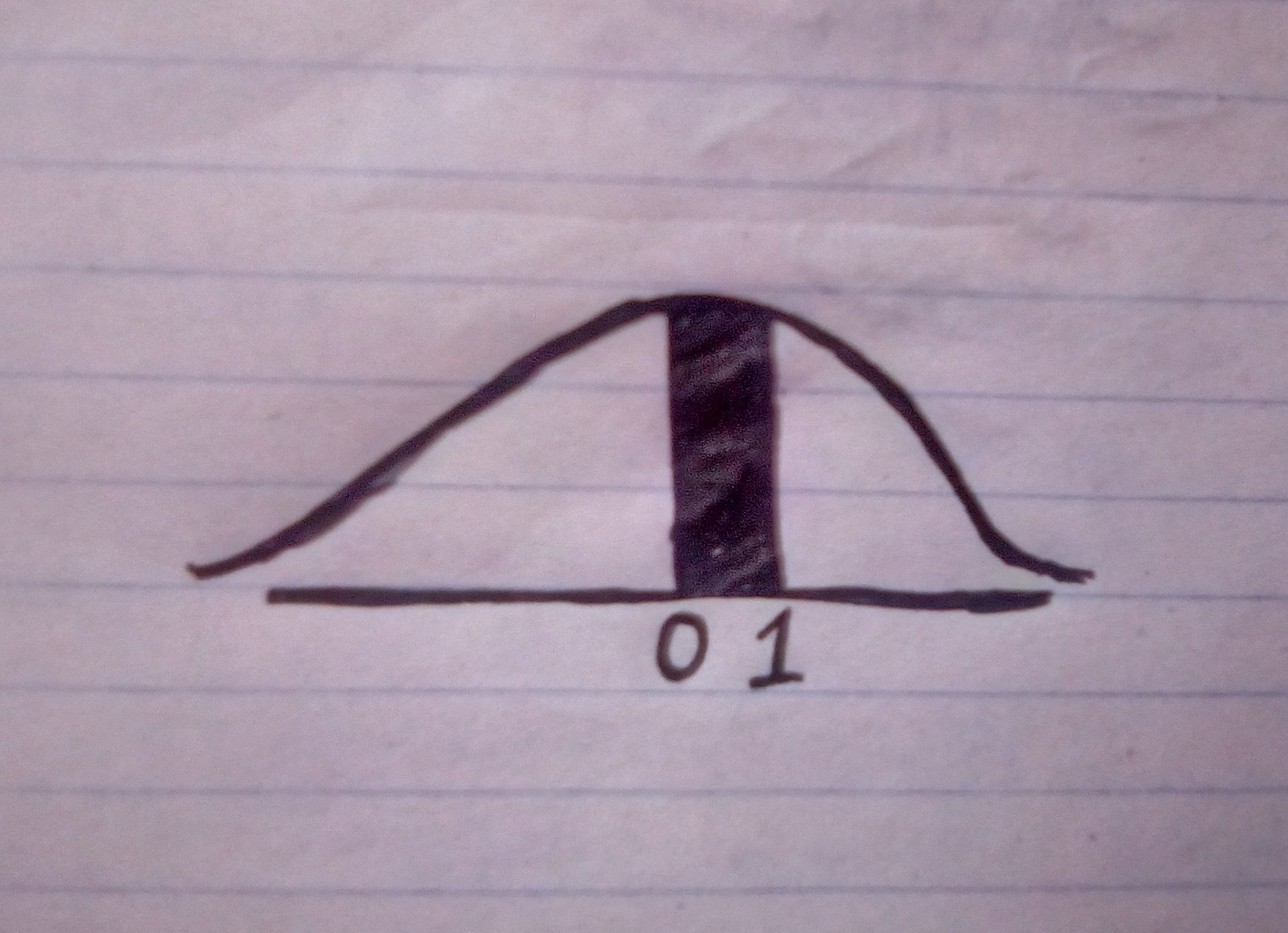

( Noted ) :
           Use zero ( 0 )in the center because it is already standardized.

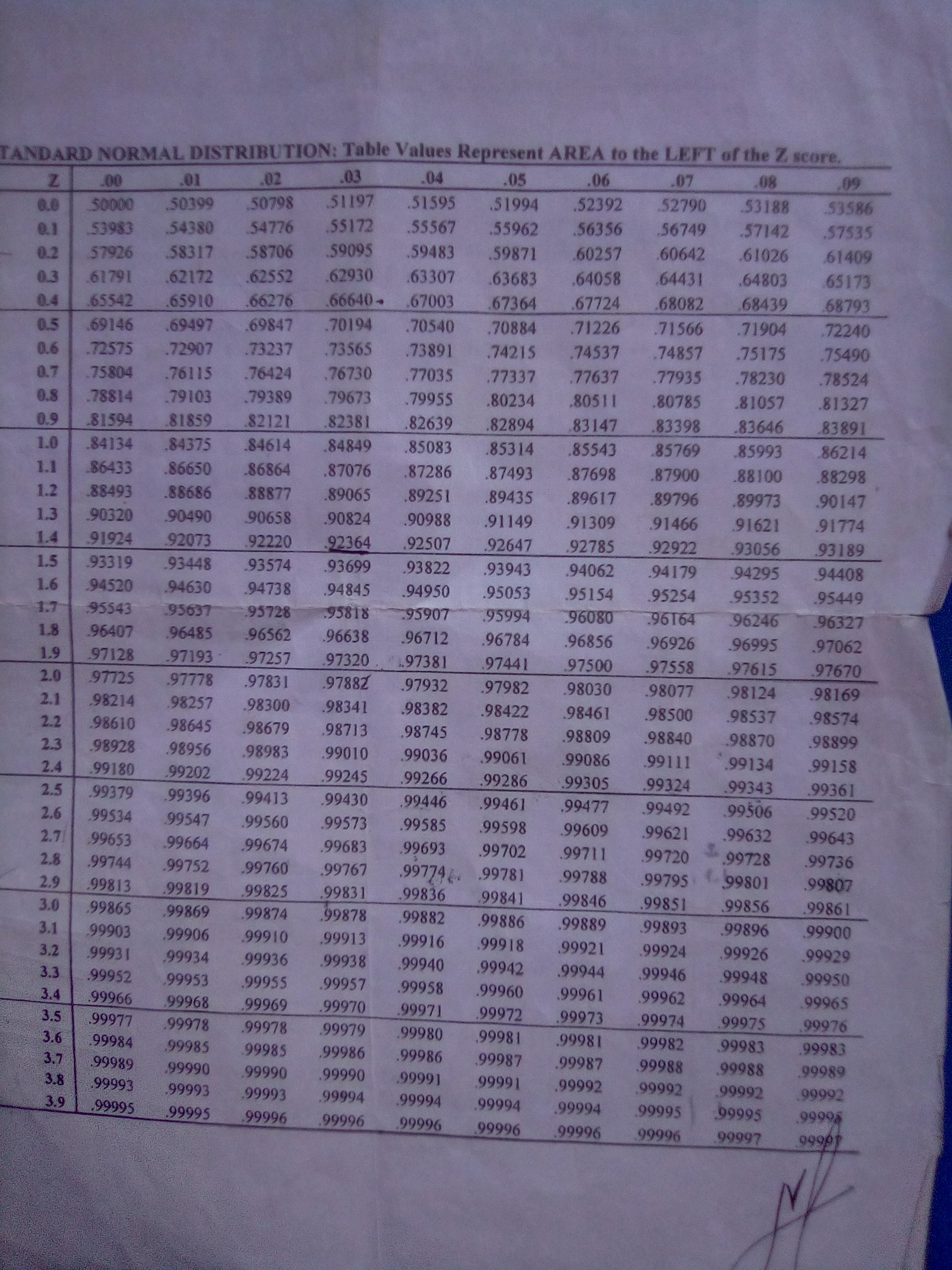
Step 9: Find the are require needed by finding it in the table of standard normal distribution.

Table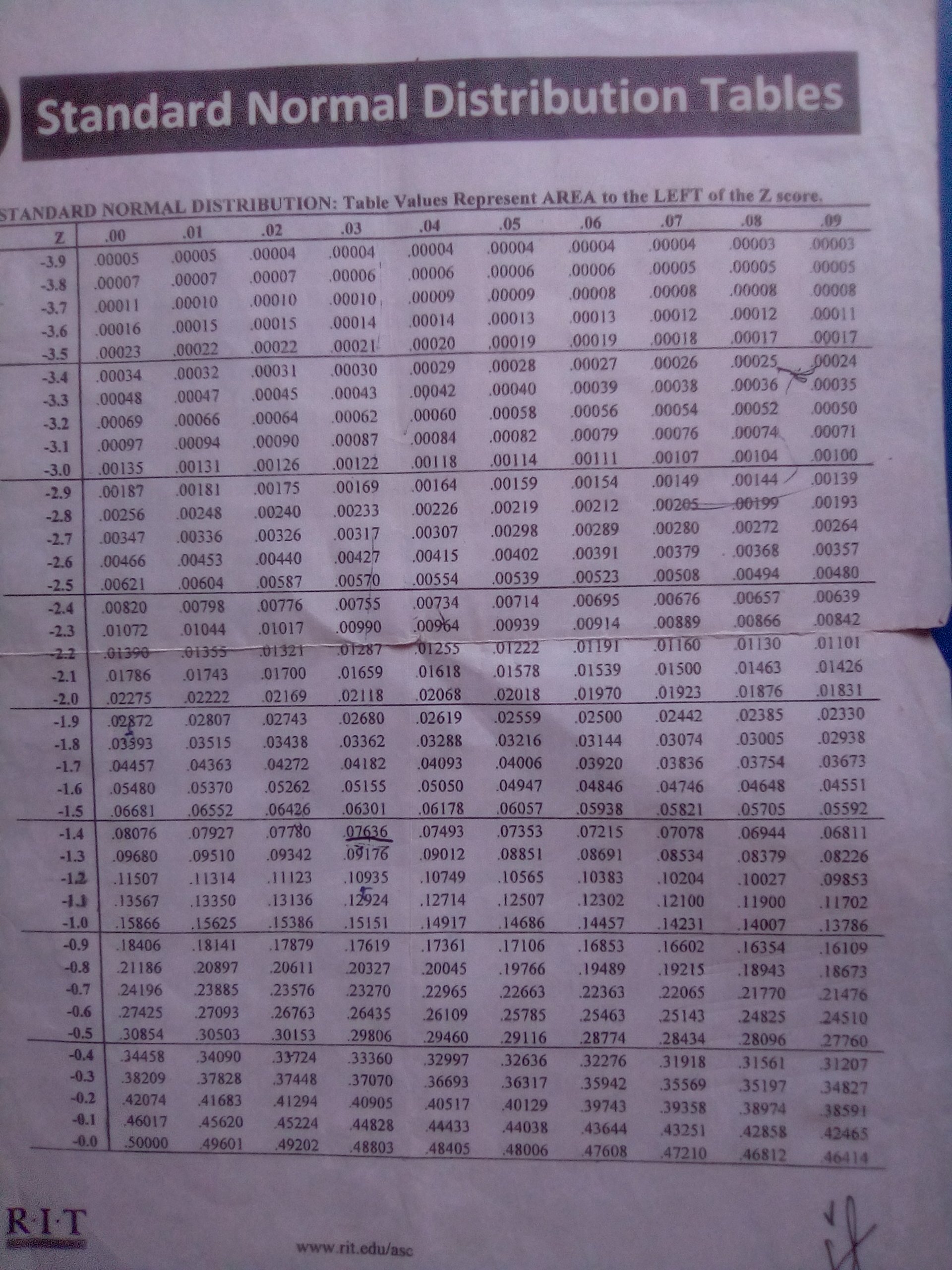
Example:
     P( 0 < Z < 1 )
     = .50000 – .84134
    = .34134 or 34.13%  – convert it to       percentage.

( Noted ) :
           Subtract the smaller number than the bigger number.

Step 10:  Answer the questions.

Example:
      The probability that battery life of gadget will last between 3 and 4 years is 34.13%